*Maydalid López Ramírez.
* Jeniffer Odalys Cortes Mendoza.
ARTICULOS
ARTÍCULO Nº 1
APLICACIÓN DE TRIÁNGULOS
Desde la antigüedad el hombre utilizó diversas formas triangulares para su supervivencia como herramientas de caza, construcciones, etc.
El triángulo
es muy utilizado en la vida diaria, basta observar a nuestro alrededor para
identificar las formas triangulares. Las formas triangulares están
presente en diferentes aplicaciones: edificaciones, instrumentos musicales,
objetos domésticos, objetos de escritorio, señales de tránsito, etc.
El triángulo
es muy utilizado en las estructuras porque es la única figura que no se puede
deformar, hagas lo que hagas seguirá siendo un triángulo.
Los triángulos
tienen una gran importancia en la geometría, pues todo polígono puede ser
descompuesto o formado por triángulos. Esta gran importancia de los triángulos
en la geometría, ya la conocían los geómetras desde los tiempos de las primeras
civilizaciones.
FUNDAMENTOS TEORICOS:
ARTÍCULO
Nº 2
"SEMEJANZA DE
TRIÁNGULOS"
Dos triangulos son semejantes si tienen sus angulos respectivamente congruentes y si sus lados homólogos son proporcionales.
Dos triangulos son semejantes si cumple cualquiera de las siguientes condiciones
Dos triangulos son semejantes si tienen sus angulos respectivamente congruentes y si sus lados homólogos son proporcionales.
Dos triangulos son semejantes si cumple cualquiera de las siguientes condiciones
1. Si tienen dos de sus ángulos iguales.
2. Si sus lados son proporcionales.
3. Si tienen un ángulo igual y sus lados
contiguos proporcionales.
-Feria/MatematicasAstronomicas/triangulos.htm
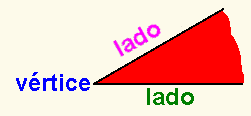
QUE ES UN ANGULO:Ángulo es la porción de plano limitada por dos semirrectas con origen en un mismo punto. Las semirrectas se llaman lado inicial y final. Al origen común se le denomina vértice del ángulo.
Los ángulos se nombran de varias maneras:
-con una letra minúscula, como a o b, o a veces con una letra griega como . (alfa)
-con tres letras mayúsculas y un símbolo en forma de ángulo encima. La letra del medio es el vértice.
Un triángulo es el polígono que resulta de unir 3 puntos con líneas rectas.
Todo triángulo tiene 3 lados
(a, b y c), 3 vértices (A, B y C) y 3 ángulos interiores (A, B y C)
Habitualmente se llama lado a
al lado que no forma parte del ángulo A. Lo mismo sucede con los lados b y c y
los ángulos B y C.
Según la medida de sus lados
- Equilátero
Los 3
lados (a, b y c) son iguales
Los 3
ángulos interiores son iguales
- Isósceles
Tienen 2 lados iguales (a y b) y un lado distinto (c)
Los
ángulos A y B son iguales, y el otro agudo es distinto
- Escaleno:
Los 3 lados son distintos
Los 3
ángulos son también distintos
Según la medida de sus
ángulos
- Acutángulo
Tienen los 3 ángulos agudos (menos de 90 grados)
- Rectángulo:
El ángulo interior A es recto (90 grados) y los otros 2 ángulos son agudos
Los
lados que forman el ángulo recto se llaman catetos (c y b), el otro lado
hipotenusa
- Obtusángulo:
El
ángulo interior A es obtuso (más de 90 grados)
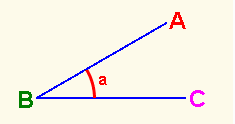
Un ángulo es la porción de plano limitada por dos semirrectas o rayos que tienen el mismo origen.
Los lados del ángulo son las semirrectas que lo forman.
El vértice del ángulo es el punto común que es origen de los lados.
Los ángulos pueden nombrarse de tres formas distintas:
Por las letras mayúsculas correspondientes a las semirrectas, colocando en medio la letra vértice:
ó 
Por una letra o número colocado en la abertura a
Por la letra del vértice B
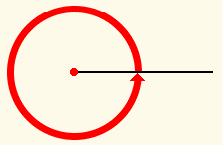
Un ángulo completo es el que está delimitado por dos semirrectas que coinciden.
La bisectriz de una ángulo es la semirrecta que divide al ángulo en dos partes iguales.
La semirrecta OA es bisectriz del ángulo O si se cumple que: 
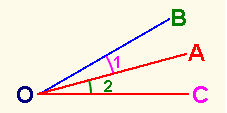
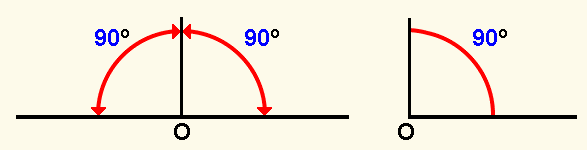
Ángulo Recto, es uno cualquiera de los ángulos en que la bisectriz divide al llano. Su amplitud o abertura es de 90º.
Agudo, es todo ángulo cuya amplitud sea menor que la del recto, es decir, es como máximo de 90º.
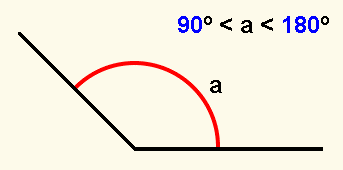
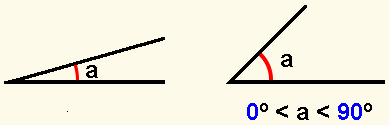Obtuso, es aquel cuya amplitud es mayor que la del ángulo recto y menor que la del llano, es decir, está comprendida entre 90º y 180º.
Cóncavo, es el que vale menos que un llano. Por ello se dice que los ángulos cóncavos comprenden a los agudos, rectos y obtusos.
El vértice del ángulo es el punto común que es origen de los lados.
Por las letras mayúsculas correspondientes a las semirrectas, colocando en medio la letra vértice:
ó Por una letra o número colocado en la abertura a
Por la letra del vértice B
Clasificación de los ángulos:
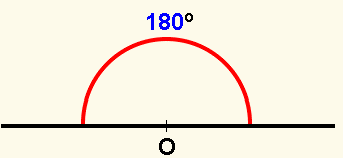
Llano, es el ángulo formado por dos semirrectas opuestas. Tiene sus lados en la misma recta. Su amplitud es la mitad de un ángulo completo, es decir, de 180º.
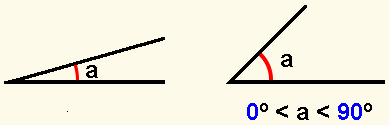
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Triangulos_propiedades_metricas/Triangulos.%20Propiedades%20metricas.htm
Ángulos complementarios, suplementarios y opuestos:
·
Dos ángulos son complementarios si su suma vale 90º
·
Dos ángulos son suplementarios si su suma vale 180º.
·
Dos ángulos son opuestos por el vértice cuando tienen el
mismo vértice y los lados de uno son semirrectas opuestas a los del otro.
Ángulos de lados paralelos
Dos ángulos que tienen los lados paralelos son:
·
Iguales, si ambos son agudos
o ambos obtusos.
Suma de los ángulos de un triángulo
·
La suma de los ángulos de un triángulo es 180º
Si observamos la escena siguiente los tres ángulos con vértice en C y
coloreados en rojo, amarillo y magenta son iguales respectivamente a A (ángulos
de lados paralelos), C y B (ángulos de lados paralelos). De la figura se deduce
que suman 180º.
Arrastra con el ratón los vértices A, B y C y comprueba cómo se
mantiene igual a 180º la suma de los ángulos.
Ángulos de lados perpendiculares
Dos ángulos que tienen los lados perpendiculares son:
·
Suplementarios, si uno es agudo y
el otro obtuso.
La
geometría y la arquitectura son dos disciplinas que están fundamentalmente
vinculadas. Una de las más reconocidas figuras geométricas es el triángulo. Los
triángulos son identificados por los tres ángulos que están conectados a través
de segmentos lineales para formar una figura de tres lados. Las dos formas de
triángulo más comunes utilizadas en arquitectura son el equilátero y el
isósceles.
Los triángulos son herramientas eficaces para la
arquitectura y se utilizan en el diseño de los edificios y otras estructuras,
ya que proporcionan resistencia y estabilidad. Cuando se utilizan materiales de construcción para formar un triángulo, el
diseño tiene una gran base y el pináculo de la parte superior es
capaz de administrar el peso porque la energía se distribuye a través de todo
el triángulo. Esta es la razón por la que muchos hogares residenciales tienen
cabriadas que proporcionan una estructura robusta. El triángulo de uso en la
arquitectura data de hace más años que otras formas comunes como el domo, arco,
cilindro, e incluso es anterior a la rueda. Los más resistentes son los
triángulos equiláteros y los isósceles; su simetría ayuda a distribuir peso.
TRIANGULACIÓN DE ESTRUCTURAS.
Existen muchas estructuras que están formadas a base de triángulos unidos entre sí. Este tipo de estructuras, que adquieren una gran rigidez, tienen infinidad de aplicaciones.
El triángulo es el único polígono que no se deforma cuando actúa sobre él una fuerza. Al aplicar una fuerza de compresión sobre uno cualquiera de los vértices de un triángulo formado por tres vigas, automáticamente las dos vigas que parten de dicho vértice quedan sometidas a dicha fuerza de compresión, mientras que la tercera quedará sometida a un esfuerzo de tracción. Cualquier otra forma geométrica que adopten los elementos de una estructura no será rígida o estable hasta que no se triangule.
Si quieres observar el efecto que tendría sobre cada uno de estas estructuras articuladas el efecto de una fuerza coloca el ratón sobre cada imagen.
En este sentido, podemos observar cómo las estanterías metálicas desmontables llevan para su ensamblado unas escuadras o triángulos, que servirán como elemento estabilizador al atornillarse en los vértices correspondientes. Análogamente, en los andamios de la construcción se utilizan tirantes en forma de aspa, que triangulan la estructura global y le confieren
A base de triangulación se han conseguido vigas de una gran longitud y resistencia, que se llaman vigas reticuladas o arriostradas y que se emplean profusamente en la construcción de grandes edificaciones que necesitan amplias zonas voladas y sin pilares, así como en la de puentes de una gran luz. Las vigas de este tipo tienen una mayor resistencia que las vigas macizas.
Sin duda la estructura reticulada más famosa del mundo es la torre Eiffel. El ingeniero civil francés Alexandre Gustave Eiffel la proyectó para la Exposición Universal de París de 1889. El edificio, sin su moderna antena de telecomunicaciones, mide unos 300 m de altura. La base consiste en cuatro enormes arcos que descansan sobre cuatro pilares situados en los vértices de un rectángulo. A medida que la torre se eleva, los pilares se giran hacia el interior, hasta unirse en un solo elemento articulado. Cuenta con escaleras y ascensores (elevadores), y en su recorrido se alzan tres plataformas a distintos niveles, cada una con un mirador, y la primera, además, con un restaurante. Para su construcción se emplearon unas 6.300 toneladas de hierro. Cerca del extremo de la torre se sitúan una estación meteorológica, una estación de radio, una antena de transmisión para la televisión y unas habitaciones en las que vivió el propio Eiffel.
Criterios de congruencia de triángulos
Los criterios de congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos.
Primer criterio de congruencia: LLL
Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’
Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’
Segundo criterio de congruencia: LAL
Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’
Tercer criterio de congruencia: ALA
Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
Dos triángulos son congruentes si tienen dos lados respectivamente congruentes y los ángulos opuestos al mayor de los lados también son congruentes.
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
ENTREVISTA:
1- ¿Es importante el uso de los triángulos en su vida cotidiana?
R: Si
2- ¿Por qué?
2- ¿Por qué?
R: porque nos sirve para construir empresas o construcciones.
3- ¿En qué partes podemos hacer el uso de los triángulos?
R: En un parque de diversiones, en una casa, un hotel, una rebanada de pizza, una rebanada de pastel, etc.
4- ¿Cree que es importante tomar en cuenta los ángulos de un triángulo?
R: Si
5- ¿Por qué?
R: Porque asi podemos calcular lo que queremos hacer.
6- ¿Considera que algunas personas necesitan saber las medidas de los triángulos?
R: Si
7- ¿Por qué?
R: Porque los ingenieros lo utilizan para la construcción de algunas obras o construcciones grandes y pequeñas.
8- ¿Quiénes son las personas que utilizan mas las medidas de los triángulos?
R: Los ingenieros, los arquitectos y los estudiantes de la materia de matemáticas.
R: Si
R: Porque si quieren estudiar algo relacionado con ello lo tienen que aprender bien o solo para la gran utilización de su vida diaria.
ag
ResponderEliminargracias esto me ayudo mucho para mi tarea
ResponderEliminarNo me sirvio para nada, deberian especificarse más con lo que quisierón decir, espero que este comentario le sirva para que mejoren lo que quisieron referirse, muchas gracias!
ResponderEliminarCasino Hotel Philadelphia - Mapyro
ResponderEliminarCasino 밀양 출장마사지 Hotel Philadelphia location map and reviews. Book now - 제주도 출장마사지 online 강릉 출장안마 with Mapyro to 의왕 출장안마 find the best deal for 여수 출장마사지 your trip. Search by area or by state - view the